Vocabulary
Circle-a shape with all points the same distance from its center.
Point-A circle is a shape with all points the same distance from its center. A circle is named by its center point. Some real world examples of a circle are a wheel, a dinner plate and (the surface of) a coin.
Diameter-The distance across a circle through the center.
Radius-the distance from the center of a circle to any point on the circle. The plural is Radii.
Chord-A chord is a line segment that joins two points on a curve.
Examples
How to Calculate the Area
| The area of a circle is π (Pi) times the Radius squared, which is written: |
A = π × r2
|
|
| Or, when you know the Diameter: |
A = (π/4) × D2
|
|
| Or, when you know the Circumference: |
A = C2 / 4π
|
Example: What is the area of a circle with radius of 3 m ?
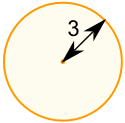
Radius = r = 3
| Area | = π × r2 | |
| = π × 32 | ||
| = π × (3 × 3) | ||
| = 3.14159... × 9 | ||
| = 28.27 m2 (to 2 decimal places) |
How to Remember?
To help you remember think "Pie Are Squared"
(even though pies are usually round)
Comparing a Circle to a Square
It is interesting to compare the area of a circle to a square:
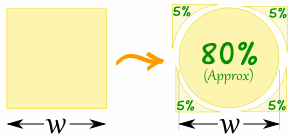
A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%
The actual value is (π/4) = 0.785398... = 78.5398...%
Why? Because the Square's Area is w2
and the Circle's Area is (π/4) × w2
and the Circle's Area is (π/4) × w2
Example: Compare a square to a circle of width 3 m
Square's Area = w2 = 32 = 9 m2Estimate of Circle's Area = 80% of Square's Area = 80% of 9 = 7.2 m2
Circle's True Area = (π/4) × D2 = (π/4) × 32 = 7.07 m2 (to 2 decimals)
The estimate of 7.2 m2 is not far off 7.07 m2
A "Real World" Example
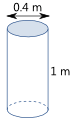
Example: Max is building a house. The first step is to drill holes and fill them with concrete.
The holes are 0.4 m wide and 1 m deep, how much concrete should Max order for each hole?

The holes are circular (in cross section) because they are drilled out using an auger.
The diameter is 0.4m, so the Area will be:
A = (π/4) × D2
A = (3.14159.../4) × 0.42
A = 0.7854... × 0.16
A = 0.126 m2 (to 3 decimals)
And the holes are 1 m deep, so:
Volume = 0.126 m2 × 1 m = 0.126 m3
So Max should order 0.126 cubic meters of concrete to fill each hole.
Note: Max could have estimated the area by:
- 1. Calculating a square hole: 0.4 × 0.4 = 0.16 m2
- 2. Taking 80% of that (estimates a circle): 80% × 0.16 m2 = 0.128 m2
- 3. And the volume of a 1 m deep hole is: 0.128 m3
Video Help

No comments:
Post a Comment