Solving Inequalities by Adding or Subtracting (12-5)

Solving Inequalities by Adding or Subtracting

Vocabulary

Inequality- states that two quantities either are not equal or may not be equal.

Algebraic Inequality- an inequality that contains a variable. A value of the variable makes the
                                   inequality true is a solution of the inequality.

Solution Set- an inequality may have more than one solution. Together, all of the solutions are the
                      solution set.

Compound Inequality- the result of combing two inequalities. The words and and or are used to
                                     describe how the two parts are related.

Examples

Sometimes we need to solve Inequalities like these:

Symbol	Words	Example
>	greater than	x + 3 > 2
<	less than	7x < 28
≥	greater than or equal to	5 ≥ x - 1
≤	less than or equal to	2y + 1 ≤ 7

Solving

Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:

Something like:		x < 5
or:		y ≥ 11

We call that "solved".

How to Solve

Solving inequalities is very like solving equations ... we do most of the same things ...

... but we must also pay attention to the direction of the inequality.

Direction: Which way the arrow "points"

Some things we do will change the direction!

< would become >

> would become <

≤ would become ≥

≥ would become ≤

Safe Things To Do

These are things we can do without affecting the direction of the inequality:

Add (or subtract) a number from both sides
Multiply (or divide) both sides by a positive number
Simplify a side

Example: 3x < 7+3

We can simplify 7+3 without affecting the inequality:

3x < 10

But these things will change the direction of the inequality ("<" becomes ">" for example):

Multiply (or divide) both sides by a negative number
Swapping left and right hand sides

Example: 2y+7 < 12

When we swap the left and right hand sides, we must also change the direction of the inequality:

12 > 2y+7

Here are the details:

Adding or Subtracting a Value

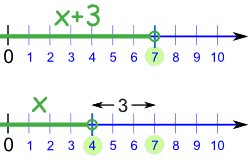
We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra), like this:

Solve: x + 3 < 7

If we subtract 3 from both sides, we get:

x + 3 - 3 < 7 - 3    

x < 4

And that is our solution: x < 4
In other words, x can be any value less than 4.

What did we do?

We went from this: To this:				x+3 < 7 x < 4

And that works well for adding and subtracting, because if we add (or subtract) the same amount from both sides, it does not affect the inequality

Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?

No matter, just swap sides, but reverse the sign so it still "points at" the correct value!

Example: 12 < x + 5
If we subtract 5 from both sides, we get:

12 - 5 < x + 5 - 5    

7 < x

That is a solution!
But it is normal to put "x" on the left hand side ...

... so let us flip sides (and the inequality sign!):

x > 7

Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7

Note: "x" can be on the right, but people usually like to see it on the left hand side.

http://www.mathsisfun.com/algebra/inequality-solving.html

Video Help

https://www.youtube.com/watch?v=UTs4uZhu5t8

https://www.youtube.com/watch?v=1Z22Xh66VFM

https://www.youtube.com/watch?v=nuI1eRZR_gU