Adding and Subtracting Fractions (3-7)

Adding and Subtracting  Fractions

Vocabulary

Numerator - The number of expression written above the line in a fraction.

Denominator - The quantity below the line in a fraction, telling the number of equal parts the whole is
divided into.

Common Denominator - The same number on the bottom of all fractions involved in the equation.

Simplify - Combine like terms and apply properties to an expression to make computation easier.

Equivalent - Naming the same number.

Before you can add or subtract fractions with different denominators, you must first find equivalent fractions with the same denominator, like this:

1. Find the smallest multiple (LCM) of both numbers.
2. Rewrite the fractions as equivalent fractions with the LCM as the denominator.

A FRACTION IS A number we need for measuring; therefore we sometimes have to add or subtract them. Now, to add or subtract anything, the names of what we are counting -- the units -- must be the same. 2 apples + 3 apples = 5 apples. We cannot add 2 apples plus 3 oranges -- at least not until we call them "pieces of fruit." In the name of a fraction -- "2 ninths," for example -- ninths are what we are adding. 2 ninths + 3 ninths = 5 ninths. That unit appears as the denominator.

1.   How do we add or subtract fractions? The names of what we are adding or subtracting -- the denominators -- must be the same.  Add or subtract only the numerators, and keep that same denominator.

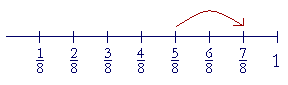
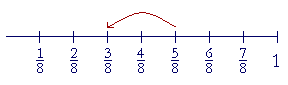
Example 1.    5 8  +  2 8  =  7 8 . "5 eighths + 2 eighths = 7 eighths." The denominator of a fraction has but one function, which is to name what we are counting.  In this example, we are counting eighths.   Example 2.    5 8  −  2 8  =  3 8 . Fractions with different denominators To add or subtract fractions, the denominators must be the same.  Before continuing, then, the student should know how to convert one fraction to an equivalent one, by multiplying the numerator and the denominator.

2.   How do we add fractions with different denominators? 2 3   +   1 4 Convert each fraction to an equivalent fraction with the same denominator.

3.   What number should we choose as the common denominator?   Choose a common multiple of the original denominators. Choose their lowest common multiple.

We choose a common multiple of the denominators because we change a denominator by multiplying it.    Example 3.      2 3  +  1 4 . Solution.  The lowest common multiple of 3 and 4 is their product, 12. We will convert each fraction to an equivalent fraction with denominator 12. 2 3  +  1 4  =   8  12  +   3  12  =  11 12 .  We converted   2 3  to   8  12   by saying, "3 goes into 12 four times. Four times 2 is 8." (In that way, we multiplied both 2 and 3 by the same number, namely 4.  We converted   1 4  to   3  12   by saying, "4 goes into 12 three times.  Three times 1 is 3."  (We multiplied both 1 and 4 by 3.) The fact that we say what we do shows again that arithmetic is a spoken skill. In practice, it is necessary to write the common denominator only once: 2 3  +  1 4  =  8 + 3   12  =  11 12 .   Example 4.     4 5  +   2  15 Solution.  The LCM of 5 and 15  is 15.  Therefore, 4 5  +   2  15  =  12  +  2     15  =  14 15 . We changed   4 5  to  12 15   by saying, "5 goes into 15 three times. Three times 4 is 12." We did not change   2  15  , because we are not changing the denominator 15.   Example 5.      2 3  +  1 6  +   7  12 Solution.  The LCM of 3, 6, and 12  is 12. 2 3  +  1 6  +   7  12   =   8 + 2 + 7      12 2 3  +  1 6  +   7 12   =   17 12 2 3  +  1 6  +   7 12   =  1  5  12 . We converted   2 3   to    8  12   by saying, "3 goes into 12 four times.  Four times 2 is 8." We converted   1 6   to    2  12   by saying, "6 goes into 12 two times.  Two times 1 is 2."   We did not change   7  12  , because we are not changing the denominator 12. Finally, we changed the improper fraction   17 12   to  1  5  12   by dividing 17 by 12. "12 goes into 17 one (1) time with remainder 5."   Example 6.     5 6  +  7 9 Solution.  The LCM of 6 and 9  is 18. 5 6  +  7 9   =   15 + 14    18   =   29 18   =  1 11 18 . We changed   5 6   to   15 18   by multiplying both terms by 3. We changed   7 9   to   14 18   by multiplying both terms by 2.   Example 7.    Add mentally   1 2  +  1 4 .   Answer.    1 2  is how many  1 4 's? 1 2  =  2 4 . Just as 1 is half of 2, so 2 is half of 4.  Therefore, 1 2  +  1 4  =  3 4 . The student should not have to write any problem in which one of   the fractions is  1 2 , and the denominator of the other is even. For example, 1 2  +   2  10  =   7  10   -- because   1 2  =   5  10 . Example 8.   In a recent exam, one eighth of the students got A, two fifths got B, and the rest got C.  What fraction got C?  Solution.   Let 1 represent the whole number of students.  Then the question is: 1 8  +  2 5  + ?  = 1 . Now, 1 8  +  2 5  =  5 + 16    40  =  21 40 . The rest, the fraction that got C, is the complement of   21 40 . It is  19 40 . http://www.themathpage.com/arith/add-fractions-subtract-fractions-1.htm Video Help https://www.youtube.com/watch?v=GFGlgSfQ-Gk https://www.youtube.com/watch?v=52ZlXsFJULI https://www.youtube.com/watch?v=t6Gz2zwmeD0