Vocabulary
Coordinate Plane- a plane containing a horizontal number line and a vertical number line.
X-axis- a horizontal number line on a coordinate plane. The left side is negative, the right side is
positive.
Y-axis- a vertical number line on a coordinate plane. The upper portion is positive and the lower
portion is negative.
Origin- The intersecting point of the x and y axis.
Quadrant- four equal regions on a coordinate plane created by the placement of the x and y axis.
Ordered Pair- a pair of numbers that can be used to locate a specific point on a coordinate plane.
Function- operates according to a rule to produce exactly one output value for each input.
Input- the value substituted into the function.
Output- the value that results from the substitution of a given input into the function.
Sequence- an ordered list of numbers.
Term- each number within a sequence.
Arithmetic Sequence- a set of numbers in which the difference between any two numbers are the
same.
Common Difference- the terms of the sequence differ by the same nonzero number.
Geometric Sequence- each term is multiplied by the same amount to get the next term in the
sequence.
Linear Equations- an equation whose graph is a line.
Linear Function- a function whose graph is a non-vertical line.
Slope- The measured steepness of a line and is the ratio rise to run.
Rate of Change- the ratio of two quantities that change, such as a slope.
X-Intercept- the x-coordinate of the point where the line intersects the x-axis. The y-coordinate of
this point is always zero.
Y-Intercept- the y-coordinate of the point where the line intersects the y-axis. The x-coordinate of
this point is always zero.
Slope-Intercept Form- the linear equation y = mx +b ; m is the slope and b is the y-intercept of the
line
Examples
The mathematical definition of slope is very similar to our everyday one. In math, slope is the ratio
of the vertical and horizontal changes between two points on a surface
or a line. The vertical change between two points is called the rise, and the horizontal change is called the run. The slope equals the rise divided by the run: 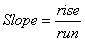 . This simple equation is called the slope formula.
. This simple equation is called the slope formula.
The
slope formula is often shortened to the phrase “rise over run.”
Although it sounds simple, the slope formula is a powerful tool for
calculating and comparing the steepness of landscapes, structures, and
lines.
Rate of Change
Connecting Slope to Real Life
The slope of a line tells us how something changes over time. If we find the slope we can find the rate of change over that period.
take a look
 at the following graph.
at the following graph.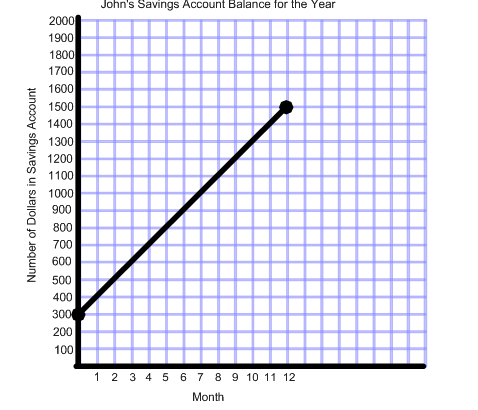
 balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.
balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.John may want to analyze his finances
 a little more and figure out about how much he was saving per month. This is called the rate of change per month.
a little more and figure out about how much he was saving per month. This is called the rate of change per month.By finding the slope of the line, we would be calculating
 the rate of change.
the rate of change.We can't count the rise over the run like we did in the calculating slope lesson because our units on the x and y axis are not the same. In most real life problems, your
 units will not be the same on the x and y axis. So, we need another method!
units will not be the same on the x and y axis. So, we need another method!We will need to use a formula for finding slope given two points.
Finding Slope Given Two Points
Rate of Change
Connecting Slope to Real Life
The slope of a line tells us how something changes over time. If we find the slope we can find the rate of change over that period.
take a look
 at the following graph.
at the following graph.
 balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.
balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.John may want to analyze his finances
 a little more and figure out about how much he was saving per month. This is called the rate of change per month.
a little more and figure out about how much he was saving per month. This is called the rate of change per month.By finding the slope of the line, we would be calculating
 the rate of change.
the rate of change.We can't count the rise over the run like we did in the calculating slope lesson because our units on the x and y axis are not the same. In most real life problems, your
 units will not be the same on the x and y axis. So, we need another method!
units will not be the same on the x and y axis. So, we need another method!We will need to use a formula for finding slope given two points.
Finding Slope Given Two Points

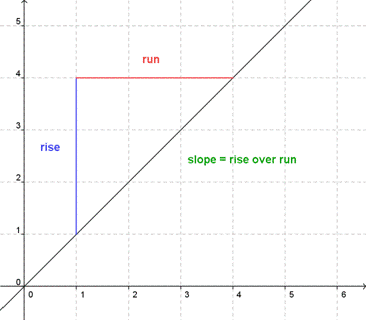
We can find the slope of a line on a graph by counting off the rise and the run between two points. If a line rises 4 units for every 1 unit that it runs, the slope is 4 divided by 1, or 4. A large number like this indicates a steep slope: in this case, the slope goes 4 steps up for every one step sideways.
If a line rises 2 units while it runs
8 units, the slope is 2 divided by 8, or ¼. A small number like this
represents a gentle slope. This line goes up only 1 step while it
travels 4 steps to the side.
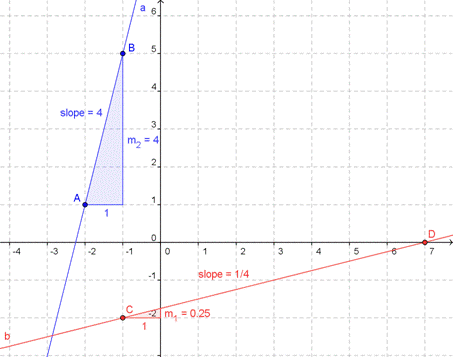
The ratio
of rise over run describes the slope of all straight lines. This ratio
is constant between any two points along a straight line, which means
that the slope of a straight line is constant, too, no matter where it
is measured along the line.
It’s
easy to find the slope of a line on a graph by measuring the rise and
the run. We can also find the slope of a straight line if we know the coordinates of any two points on that line. Every point has a set of coordinates: a y-value and an x-value, written as (x, y). The x value tells us where a point is horizontally. The y value tells us where the point is vertically.
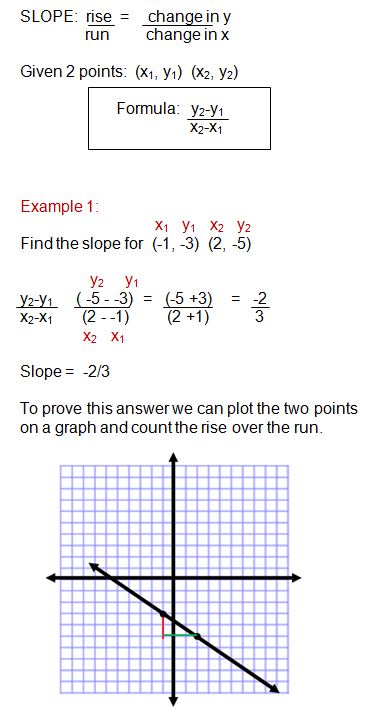
Consider two random points on a line. We’ll call them point 1 and point 2. Point 1 has coordinates (x1, y1) and point 2 has coordinates (x2, y2).
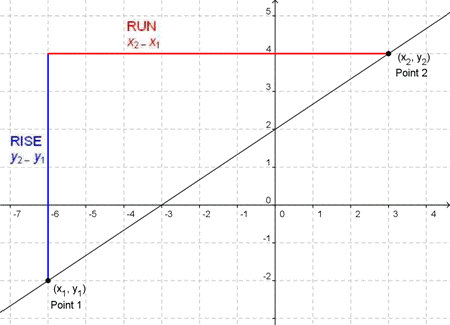
The rise is the vertical distance between the two points, which is the difference between their y-coordinates. That makes the rise y2 − y1. The run between these two points is the difference in the x-coordinates, or x2 − x1. Since slope equals rise over run, the slope of the line is y2 − y1 over x2 − x1. We’ve now got a new way to write the slope formula and to calculate the value of a slope. Slope is the difference between the y-coordinates divided by the difference between the x-coordinates.
Mathematicians commonly use the letter m to represent slope. So this is how you will most often see the slope formula written in algebra: 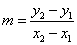 . At heart, though, this is still the simple equation of slope = rise over run.
. At heart, though, this is still the simple equation of slope = rise over run.
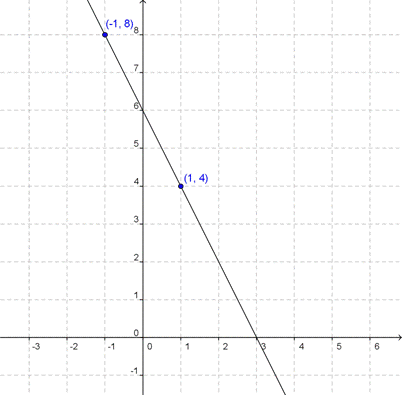
Let’s
use the slope formula to calculate the slope of a line, using just the
coordinates of two points. The line passes through the points (1, 4) and
(-1, 8). Let’s call the point (1, 4) point 1, and the point (-1, 8)
point 2. That means x1 = 1, y1 = 4, x2 = -1, and y2 = 8.
Example
| |
Points
|
Coordinates
|
(1, 4)
|
x1 = 1
y1 = 4
|
(-1, 8)
|
x2 = -1
y2 = 8
|
The slope formula is 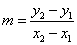 . When we put the coordinates into the formula, we get the equation
. When we put the coordinates into the formula, we get the equation 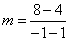 . This reduces to m = -2. The slope of the line is -2.
. This reduces to m = -2. The slope of the line is -2.
It
is important to realize that it doesn’t matter which point is
designated as 1 and which is 2. We could have called (-1, 8) point 1,
and (1, 4) point 2. In that case, putting the coordinates into the slope
formula produces the equation 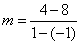 . Once again, that simplifies to m = -2. That’s the same slope as before.
. Once again, that simplifies to m = -2. That’s the same slope as before.
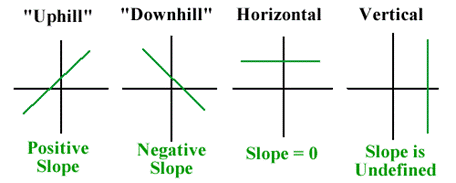
So
far we’ve considered lines that run “uphill” or “downhill.” Their
slopes may be large or small, but they are always positive or negative
numbers. But there are two other kinds of lines, horizontal and
vertical. What is the slope of a flat line or level ground? Of a sheer wall or a vertical line?
Let’s
consider a horizontal line on a graph. No matter which two points we
choose on the line, they will always have the same y-coordinate.
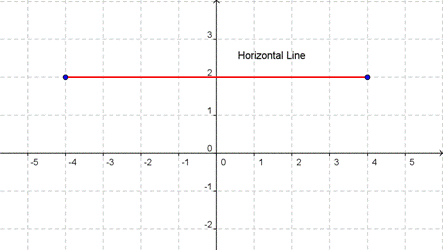
That
means the rise, the vertical difference between two points, will always
be zero. That makes sense—a horizontal line doesn’t go up or down. What
happens when we put a rise of 0 into the slope formula? It becomes 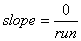 . Zero divided by any number is zero. The slope of a horizontal line is always 0.
. Zero divided by any number is zero. The slope of a horizontal line is always 0.
How about vertical lines? In their case, no matter which two points we choose, they will always have the same x-coordinate,
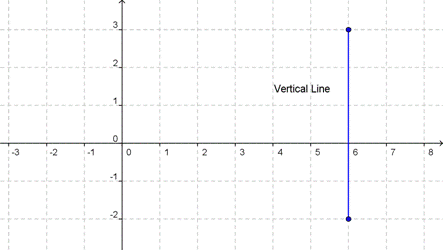
That
means that the run, the horizontal difference between two points, will
always be zero. That makes sense—a vertical line doesn’t go sideways at
all. When we put a run of 0 into the slope formula, the equation becomes
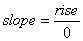 . We can’t calculate that value because division by zero has no meaning in the set of real numbers. All vertical lines have a slope that is undefined.
. We can’t calculate that value because division by zero has no meaning in the set of real numbers. All vertical lines have a slope that is undefined.
http://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U04_L1_T1_text_final.html
Video Help
https://www.youtube.com/watch?v=Iqws-qzyZwc
https://www.youtube.com/watch?v=Ah6GNmzx3AI
https://www.youtube.com/watch?v=uzzJsU0NtAw
Rate of Change
Connecting Slope to Real Life
The slope of a line tells us how something changes over time. If we find the slope we can find the rate of change over that period.
take a look
 at the following graph.
at the following graph.
 balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.
balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.John may want to analyze his finances
 a little more and figure out about how much he was saving per month. This is called the rate of change per month.
a little more and figure out about how much he was saving per month. This is called the rate of change per month.By finding the slope of the line, we would be calculating
 the rate of change.
the rate of change.We can't count the rise over the run like we did in the calculating slope lesson because our units on the x and y axis are not the same. In most real life problems, your
 units will not be the same on the x and y axis. So, we need another method!
units will not be the same on the x and y axis. So, we need another method!We will need to use a formula for finding slope given two points.
Finding Slope Given Two Points

Rate of Change
Connecting Slope to Real Life
The slope of a line tells us how something changes over time. If we find the slope we can find the rate of change over that period.
take a look
 at the following graph.
at the following graph.
 balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.
balance has changed over the course of a year. We can see that he
opened his account with $300 and by the end of the first month
he had saved $100. By the end of the 12 month time span, John had $1500
in his savings account.John may want to analyze his finances
 a little more and figure out about how much he was saving per month. This is called the rate of change per month.
a little more and figure out about how much he was saving per month. This is called the rate of change per month.By finding the slope of the line, we would be calculating
 the rate of change.
the rate of change.We can't count the rise over the run like we did in the calculating slope lesson because our units on the x and y axis are not the same. In most real life problems, your
 units will not be the same on the x and y axis. So, we need another method!
units will not be the same on the x and y axis. So, we need another method!We will need to use a formula for finding slope given two points.
Finding Slope Given Two Points

No comments:
Post a Comment