Mathematics 4 Life and Beyond: Classifying Quadrilaterals (8-7)

Classifying Quadrilaterals

Vocabulary

Parallelogram- Opposite sides are parallel and congruent. Opposite angles are congruent.

Rectangle- Parallelogram with four right angles.

Rhombus- Parallelogram with four congruent sides.

Square- Parallelogram four congruent sides and four right angles.

Trapezoid- Exactly one pair of opposite sides is parallel.

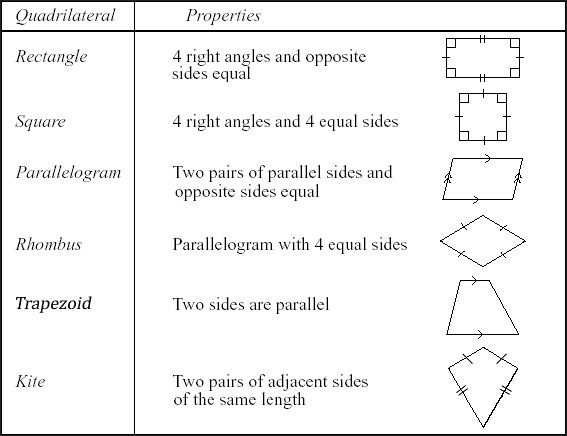
Examples

A quadrilateral is a polygon with four sides.
There are many special

types of quadrilateral.
A parallelogram is a quadrilateral in which both pairs of opposite sides are parallel.

A parallelogram also has the following properties:

Opposite angles are congruent;
Opposite sides are congruent;
Adjacent angles are supplementary;
The diagonals bisect each other.

A rectangle is a parallelogram with four right angles, so all rectangles are also parallelograms and quadrilaterals. On the other hand, not all quadrilaterals and parallelograms are rectangles.

A rectangle has all the properties of a parallelogram, plus the following:

The diagonals are congruent.

A rhombus is a parallelogram with four congruent sides. The plural of rhombus is rhombi. (I love that word.)

A rhombus has all the properties of a parallelogram, plus the following:

The diagonals intersect at right angles.

A square can be defined as a rhombus which is also a rectangle – in other words, a parallelogram with four congruent sides and four right angles.

A trapezoid is a quadrilateral with exactly one pair of parallel sides. (There may be some confusion about this word depending on which country you're in. In India and Britain, they say trapezium; in America

, trapezium usually means a quadrilateral with no parallel sides.)

An isosceles trapezoid is a trapezoid whose non-parallel sides are congruent.

A kite is a quadrilateral with exactly two pairs of adjacent congruent sides. (This definition excludes rhombi. Some textbooks say a kite has at least two pairs of adjacent congruent sides, so a rhombus is a special

case of a kite.)