Vocabulary
Product - The answer to a multiplication problem.
Reduce - Replace the fraction with its simplest form
Greatest Common Factor (GCF) - The largest factor of two or more numbers.
Cross Canceling - When multiplying fractions you can reduce the numerator of one fraction with the denominator of another.
Multiplication of fractions
is pretty simple compared to addition and subtraction. And guess what,
you don't have to find a common denominator. Just follow these four
easy steps:
Cross-canceling means that when multiplying fractions you can reduce the numerator of one fraction with the denominator of another. In this example, 5 and 10 can both be divided by 5.
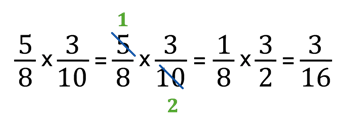
Let's look at the three examples again and see how to use this method.
Let's look at an example, shall we?

http://www.shmoop.com/fractions-decimals/multiplying-fractions-mixed-numbers.html
VIDEO HELP
https://www.youtube.com/watch?v=p729tFmpOXg
https://www.youtube.com/watch?v=zB7UTvg2VuM
https://www.youtube.com/watch?v=Svm0igHraBs
- Convert all mixed numbers to improper fractions.
- Multiply the numerators.
- Multiply the denominators.
- Reduce your final answer.
Multiplication Example 1
 | First convert 3½ to an improper fraction |
 | Next multiply the numerators, then multiply the denominators |
 | This is your answer |
 | If you'd like, you could convert that into a mixed number |
Multiplication Example 2
 | Multiply the numerators, then multiply the denominators. |
 | Reduce the fraction (12 and 72 have a GCF of 12) |
 |
Cross-Canceling
Instead of reducing the fraction at the end of the problem, you can cross-cancel before you multiply.Cross-canceling means that when multiplying fractions you can reduce the numerator of one fraction with the denominator of another. In this example, 5 and 10 can both be divided by 5.

Let's look at the three examples again and see how to use this method.
Cross-Canceling Example 1
 | |
 | In this first example, we cannot use cross-canceling, since 5 and 2 do not share a common factor, and neither do 7 and 6 |
 | |
 |
Cross-Canceling Example 2
 | |
 | Here we can reduce the 3 and 9 (by 3) and we can also reduce the 4 and 8 (by 4) |
 |
Cross-Canceling Example 3
 | First convert each to an improper fraction |
 | 14 and 7 can each be reduced by 7 |
 | Cross cancel |
 | Here's the answer |
 | If you'd like, you can turn it back in to a mixed number |
Multiplying a Whole Number by a Fraction
Well, remember that all real numbers can be written as fractions. With a whole number, all you need to do is place it over a denominator of 1.Let's look at an example, shall we?

http://www.shmoop.com/fractions-decimals/multiplying-fractions-mixed-numbers.html
VIDEO HELP
https://www.youtube.com/watch?v=p729tFmpOXg
https://www.youtube.com/watch?v=zB7UTvg2VuM
https://www.youtube.com/watch?v=Svm0igHraBs


No comments:
Post a Comment