Vocabulary
Composite Figure- a shape made up of simple geometric shapes.
Examples
The trick: break these figures into shapes that you know well (and whose area you know how to find).
1. Find the area of this room:
This can be done in two different ways:
| Method #1 | Method #2 |
Divide the figure into two rectangles and find all missing lengths.  The larger rectangle has an area of  The smaller rectangle has an area of  If we combine these we will find the total area:  | Draw two lines to make the figure into one large rectangle. The area of the large rectangle is  However, a  rectangle is not included in our original figure, so we need to take out the area of the white rectangle(  ) |
2. Find the area of this portion of a basketball court:
This figure is already divided into two shapes: a rectangle and half a circle.
We need to find the area of each and add them together.
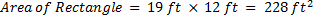
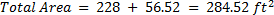
3. A 20 foot x 12 foot pool is to be surrounded by a deck 6 feet in width. How many square feet of decking is needed to do this?
As always, we want to draw a picture of what this looks like.
The dimensions of the large outside rectangle are:
So, the area of the larger rectangle is
.This amount includes the area of the pool, which we would not want to have decking. So, subtract out the area of the pool(
).The amount of decking we need is :
!http://www.shmoop.com/basic-geometry/area-irregular-shapes.html
Video Help
https://www.youtube.com/watch?v=UY8lOjAJKbo
https://www.youtube.com/watch?v=tFRCEdydcEk
https://www.youtube.com/watch?v=8HF0Nb42Eyc
No comments:
Post a Comment